Noah MacAulay

Hello, I'm Noah. This is my website featuring various projects that I've worked on.

Neural networks have proven extraordinarily succesful at a wide range of tasks. While progress has been great, our theoretical understanding of why neural networks work has lagged behind. One thing we still don't understand well is the generalization properties of neural networks, meaning how well a network will perform on new samples after being trained. If we assume that samples are independently sampled from a fixed distribution, this question becomes mathematically tractable, and it's possible to obtain generalization bounds, that is, proofs that a network will continue to perform well on new data.

Recently, some authors have used PAC-Bayes theory to obtain generalization bounds that (a) apply to neural networks trained on realistic problems such as MNIST and (b) are non-vacuous, meaning that they certify the neural network is performing better than random guessing. Obtaining both of these properties at once has proven surprisingly difficult.

In my master's thesis, I continued this line of work, using a new varitional prior to obtain generalization bounds competitive with prior work. Later, in an independent research project, I devised another variational prior based on random projections, obtaining the tighest generalization bounds yet known for MNIST. This project is being presented as a poster at the NeurIPS 2019 Workshop on Machine Learning with Guarantees.

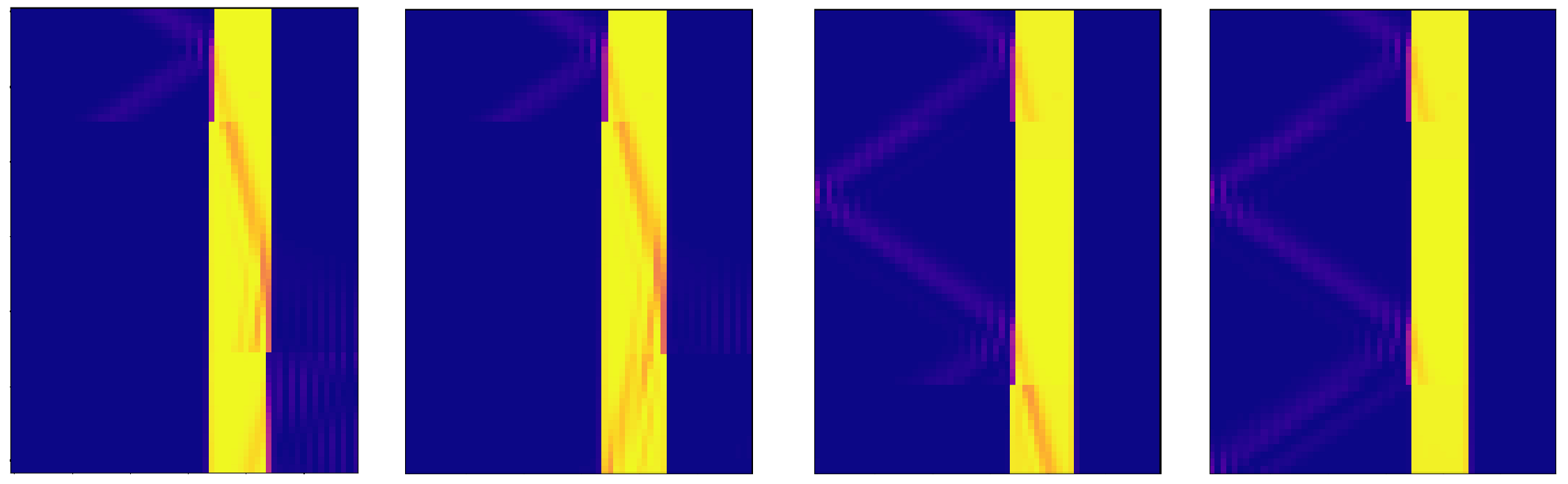
The many-worlds interpretation of quantum mechanics states that what we percieve as random wavefunction collapse is in fact the universe splitting into many different 'branches', in which different events come to pass. This idea has been around since the 60s, but there is still no first-principles definition of exactly what 'branches' are supposed to be.

For this project, I worked with a group of physicists from various institutions, with the goal of exploring a definition based on redundantly-stored information. As part of this project, I developed a novel algorithm for detecting information stored in at least three distinct sites in one-dimensional quantum systems called matrix product states. I also implemented TEBD, a popular algorithm for simulating the evolution of such systems, from scratch in Python.

Any drum head will have a set of resonant frequencies, the pure tones which the drum vibrates with when struck. These resonant frequencies depend in a delicate way on the shape of the drum head; conversely, from knowing the frequencies, it is possible to reconstruct some aspects of the shape, such as the area and circumference. From the 1960s to the 1990s, it was an open question whether it was possible to uniquely reconstruct the entirety of the drum's shape from its resonant frequencies.

It turns out the answer is no: there are pairs of drums with different shapes but the same set of resonant frequencies. My undergraduate honours' thesis reviewed the recent proof of the existence of these isospectral plane domains -- a.k.a. drums with different shapes that sound the same. The proof and its background, which cover a wide swathe of mathematics from partial differential equations to finite fields, are explained at a level that could be understood by most undergraduates.

I made some video games in high school and college using C++ and openFrameworks. They were mostly puzzle games with a philosophical bent.

The most complete one was ALIGN, a puzzle game involving placing circles on grids.

The most philosophically interesting one was SPACETIME, a puzzle game about time travel. By allowing the player to edit the entire history of spacetime, it allowed for the implementation of time paradoxes usually not possible in time travel games. Devising satisfying puzzles turned out to be hard, but I still think the underlying idea was great. I intend to go back and make a superior version at some point.

The most technically elaborate one was VISION, another puzzle game about perspective vision in 2 dimensions. There was a 2d lightcasting engine featuring mirrors(with arbitrary depth of reflection!), vision, and multicoloured light sources. Tragically, midway through development my computer crashed and I lost everything, the only remnant being a buggy prototype left on a USB stick. At this point I decided I could use a break from programming video games, and it was never completed.

In 2014, I won(?) the Lyttle Lytton contest for 'worst opening sentence of a fictitious novel'.

I also have some other humourous writing.

An attempt at explaining decoherence with interactive diagrams at an undergraduate level. Decoherence is part of the explanation for the emergence of classical reality from quantum mechanics. The interactive diagrams work best in Chrome.

I noticed a mathematical error in the paper Statistical Physics of Self-Replication. It's not clear if this error majorly affects the conclusions of the paper however.

Some pretty pictures of the Cayley graph of the discrete Heiesnberg group. I also proved that this graph contains dead ends, but I forget why this was interesting.

This website design was inspired by Adam Cadre's beautiful website.